Regency Personalities Series
In my attempts to provide us with the details of the Regency, today I continue with one of the many period notables.
Sir John Herschel
7 March 1792 – 11 May 1871

John Herschel
Herschel was born in Slough, Berkshire, the son of Mary Baldwin and William Herschel. He studied shortly at Eton College and St John’s College, Cambridge, graduating as Senior Wrangler in 1813. It was during his time as an undergraduate that he became friends with Charles Babbage and George Peacock. He took up astronomy in 1816, building a reflecting telescope with a mirror 18 inches (460 mm) in diameter and with a 20-foot (6.1 m) focal length. Between 1821 and 1823 he re-examined, with James South, the double stars catalogued by his father. For this work, in 1826 he was presented with the Gold Medal of the Royal Astronomical Society (which he won again in 1836), and with the Lalande Medal of the French Academy of Sciences in 1825, while in 1821 the Royal Society bestowed upon him the Copley Medal for his mathematical contributions to their Transactions. Herschel was made a Knight of the Royal Guelphic Order in 1831.
He served as President of the Royal Astronomical Society three times: 1827–1829, 1839–1841 and 1847–1849.
His A preliminary discourse on the study of natural philosophy published early in 1831 as part of Dionysius Lardner’s Cabinet cyclopædia set out methods of scientific investigation with an orderly relationship between observation and theorising. He described nature as being governed by laws which were difficult to discern or to state mathematically, and the highest aim of natural philosophy was understanding these laws through inductive reasoning, finding a single unifying explanation for a phenomenon. This became an authoritative statement with wide influence on science, particularly at the University of Cambridge where it inspired the student Charles Darwin with “a burning zeal” to contribute to this work.
He published a catalogue of his astronomical observations in 1864, as the General Catalogue of Nebulae and Clusters, a compilation of his own work and that of his father’s, expanding on the senior Hershel’s Catalogue of Nebulae. A further complementary volume was published posthumously, as the General Catalogue of 10,300 Multiple and Double Stars.
He also conceptualizes a practical contact lens design in 1823.
Declining an offer from the Duke of Sussex that they travel to South Africa on a Navy ship, Herschel and his wife paid £500 for passage on the S.S. Mountstuart Elphinstone, a ship of 611 tons, which departed from Portsmouth on 13 November 1833. The voyage to South Africa was made in order to catalogue the stars, nebulae, and other objects of the southern skies. This was to be a completion as well as extension of the survey of the northern heavens undertaken initially by his father William Herschel. He arrived in Cape Town on 15 January 1834 and set up a private 21 ft (6.4 m) telescope at Feldhausen at Claremont, a suburb of Cape Town. Amongst his other observations during this time was that of the return of Comet Halley. Herschel collaborated with Thomas Maclear, the Astronomer Royal at the Cape of Good Hope and the members of the two families became close friends.
In addition to his astronomical work, however, this voyage to a far corner of the British empire also gave Herschel an escape from the pressures under which he found himself in London, where he was one of the most sought-after of all British men of science. While in southern Africa, he engaged in a broad variety of scientific pursuits free from a sense of strong obligations to a larger scientific community. It was, he later recalled, probably the happiest time in his life.
In an extraordinary departure from astronomy, he combined his talents with those of his wife, Margaret, and between 1834 and 1838 they produced 131 botanical illustrations of fine quality, showing the Cape flora. Herschel used a camera lucida to obtain accurate outlines of the specimens and left the details to his wife. Even though their portfolio had been intended as a personal record, and despite the lack of floral dissections in the paintings, their accurate rendition makes them more valuable than contemporary collections. Some 112 of the 132 known flower studies were collected and published as “Flora Herscheliana” in 1996.
As their home during their stay in the Cape, the Herschels had selected ‘Feldhausen'(“Field Houses”), an old estate on the south-eastern side of Table Mountain. Here John set up his reflector to begin his survey of the southern skies. Herschel, meanwhile, read widely. Intrigued by the ideas of gradual formation of landscapes set out in Charles Lyell’s Principles of Geology, he wrote to Lyell on 20 February 1836 praising the book as a work that would bring “a complete revolution in [its] subject, by altering entirely the point of view in which it must thenceforward be contemplated” and opening a way for bold speculation on “that mystery of mysteries, the replacement of extinct species by others.” Herschel himself thought catastrophic extinction and renewal “an inadequate conception of the Creator” and by analogy with other intermediate causes, “the origination of fresh species, could it ever come under our cognizance, would be found to be a natural in contradistinction to a miraculous process”. He prefaced his words with the couplet:
He that on such quest would go must know not fear or failing
To coward soul or faithless heart the search were unavailing.
Taking a gradualist view of development and referring to the evolution of language, he commented
“Words are to the Anthropologist what rolled pebbles are to the Geologist — battered relics of past ages often containing within them indelible records capable of intelligent interpretation — and when we see what amount of change 2000 years has been able to produce in the languages of Greece & Italy or 1000 in those of Germany France & Spain we naturally begin to ask how long a period must have lapsed since the Chinese, the Hebrew, the Delaware & the Malesass [Malagasy] had a point in common with the German & Italian & each other — Time! Time! Time! — we must not impugn the Scripture Chronology, but we must interpret it in accordance with whatever shall appear on fair enquiry to be the truth for there cannot be two truths. And really there is scope enough: for the lives of the Patriarchs may as reasonably be extended to 5000 or 50000 years apiece as the days of Creation to as many thousand millions of years.”
The document was circulated, and Charles Babbage incorporated extracts in his ninth and unofficial Bridgewater Treatise, which postulated laws set up by a divine programmer. When HMS Beagle called at Cape Town, Captain Robert FitzRoy and the young naturalist Charles Darwin visited Herschel on 3 June 1836. Later on, Darwin would be influenced by Herschel’s writings in developing his theory advanced in The Origin of Species. In the opening lines of that work, Darwin writes that his intent is “to throw some light on the origin of species — that mystery of mysteries, as it has been called by one of our greatest philosophers”, referring to Herschel.
Herschel returned to England in 1838, was created a baronet, of Slough in the County of Buckingham, and published Results of Astronomical Observations made at the Cape of Good Hope in 1847. In this publication he proposed the names still used today for the seven then-known satellites of Saturn: Mimas, Enceladus, Tethys, Dione, Rhea, Titan, and Iapetus. In the same year, Herschel received his second Copley Medal from the Royal Society for this work. A few years later, in 1852, he proposed the names still used today for the four then-known satellites of Uranus: Ariel, Umbriel, Titania, and Oberon.
Herschel made numerous important contributions to photography. He made improvements in photographic processes, particularly in inventing the cyanotype process and variations (such as the chrysotype), the precursors of the modern blueprint process. In 1839, he made a photograph on glass, which still exists, and experimented with color reproduction, noting that rays of different parts of the spectrum tended to impart their own color to a photographic paper. Herschel made experiments using photosensitive emulsions of vegetable juices, called phytotypes and published his discoveries in the Philosophical Transactions of the Royal Society of London in 1842. He collaborated in the early 1840s with Henry Collen, portrait painter to Queen Victoria. Herschel originally discovered the platinum process on the basis of the light sensitivity of platinum salts, later developed by William Willis.
Herschel coined the term photography in 1839. He may, however, have been preceded by Brazilian Hércules Florence, who used the French equivalent, photographie, in private notes which one historian dates to 1834. Herschel was also the first to apply the terms negative and positive to photography.
He discovered sodium thiosulfate to be a solvent of silver halides in 1819, and informed Talbot and Daguerre of his discovery that this “hyposulphite of soda” (“hypo”) could be used as a photographic fixer, to “fix” pictures and make them permanent, after experimentally applying it thus in early 1839. His ground-breaking research on the subject was read at the Royal Society in London in March 1839 and January 1840.
Herschel wrote many papers and articles, including entries on meteorology, physical geography and the telescope for the eighth edition of the Encyclopædia Britannica. He also translated the Iliad of Homer.
He invented the actinometer in 1825 to measure the direct heating power of the sun’s rays, and his work with the instrument is of great importance in the early history of photochemistry.
He proposed a correction to the Gregorian calendar, making years that are multiples of 4000 not leap years, thus reducing the average length of the calendar year from 365.2425 days to 365.24225. Although this is closer to the mean tropical year of 365.24219 days, his proposal has never been adopted because the Gregorian calendar is based on the mean time between vernal equinoxes (currently 365.2424 days).
In 1836, he was elected a foreign member of the Royal Swedish Academy of Sciences.
In 1835, the New York Sun newspaper wrote a series of satiric articles that came to be known as the Great Moon Hoax, with statements falsely attributed to Herschel about his supposed discoveries of animals living on the Moon, including batlike winged humanoids.
He married Margaret Brodie Stewart (1810–1884) on 3 March 1829 at Edinburgh and was father of the following children:
- Caroline Emilia Elizabeth Herschel (31 March 1830 – 29 Jan 1909), who married Alexander Hamilton-Gordon
- Isabella Herschel (5 June 1831 – 1893)
- Sir William James Herschel, 2nd Bt. (9 January 1833 – 1917),
- Margaret Louisa Herschel (1834–1861), an accomplished artist
- Prof. Alexander Stewart Herschel (1836–1907), FRS
- Col. John Herschel FRS, FRAS, (1837–1921) surveyor
- Marie Sophie Herschel (1839–1929)
- Amelia Herschel (1841–1926) married Sir Thomas Francis Wade, diplomat and sinologist
- Julia Edith Herschel (1842–1933) married on 4 June 1878 to Captain (later Admiral) John Fiot Lee Pearse Maclear
- Matilda Rose Herschel (1844–1914)
- Francisca Herschel (1846–1932)
- Constance Ann Herschel (1855–20 June 1939)
On his death at Collingwood, his home near Hawkhurst in Kent, he was given a national funeral and buried in Westminster Abbey.

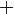 and
and  denote the operations of addition and subtraction in their ordinary meaning only, and those operations are considered as impossible in all cases where the symbols subjected to them possess values which would render them so in case they were replaced by digital numbers; thus in expressions such as
denote the operations of addition and subtraction in their ordinary meaning only, and those operations are considered as impossible in all cases where the symbols subjected to them possess values which would render them so in case they were replaced by digital numbers; thus in expressions such as  we must suppose
we must suppose 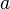 and
and 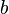 to be quantities of the same kind; in others, like
to be quantities of the same kind; in others, like  , we must suppose
, we must suppose 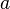 greater than
greater than 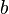 and therefore homogeneous with it; in products and quotients, like
and therefore homogeneous with it; in products and quotients, like 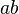 and
and 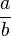 we must suppose the multiplier and divisor to be abstract numbers; all results whatsoever, including negative quantities, which are not strictly deducible as legitimate conclusions from the definitions of the several operations must be rejected as impossible, or as foreign to the science.”
we must suppose the multiplier and divisor to be abstract numbers; all results whatsoever, including negative quantities, which are not strictly deducible as legitimate conclusions from the definitions of the several operations must be rejected as impossible, or as foreign to the science.”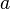 and
and 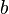 are numbers, then
are numbers, then  is always a number; but
is always a number; but  is a number only when
is a number only when 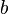 is less than
is less than 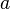 . Again, under the same conditions,
. Again, under the same conditions, 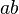 is always a number, but
is always a number, but 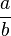 is really a number only when
is really a number only when 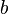 is an exact divisor of
is an exact divisor of 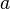 . Hence the following dilemma: Either
. Hence the following dilemma: Either 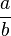 must be held to be an impossible expression in general, or else the meaning of the fundamental symbol of algebra must be extended so as to include rational fractions. If the former horn of the dilemma is chosen, arithmetical algebra becomes a mere shadow; if the latter horn is chosen, the operations of algebra cannot be defined on the supposition that the elementary symbol is an integer number. Peacock attempts to get out of the difficulty by supposing that a symbol which is used as a multiplier is always an integer number, but that a symbol in the place of the multiplicand may be a fraction. For instance, in
must be held to be an impossible expression in general, or else the meaning of the fundamental symbol of algebra must be extended so as to include rational fractions. If the former horn of the dilemma is chosen, arithmetical algebra becomes a mere shadow; if the latter horn is chosen, the operations of algebra cannot be defined on the supposition that the elementary symbol is an integer number. Peacock attempts to get out of the difficulty by supposing that a symbol which is used as a multiplier is always an integer number, but that a symbol in the place of the multiplicand may be a fraction. For instance, in 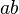 ,
, 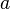 can denote only an integer number, but
can denote only an integer number, but 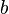 may denote a rational fraction. Now there is no more fundamental principle in arithmetical algebra than that
may denote a rational fraction. Now there is no more fundamental principle in arithmetical algebra than that  ; which would be illegitimate on Peacock’s principle.
; which would be illegitimate on Peacock’s principle.




























